Activity9

1. Foundations of Time Series Regression

We often model a response \(Y_t\) as a linear function of a predictor \(X_t\):

\[ \begin{align} Y_t &= \beta_0 + \beta_1 X_t + \varepsilon_t, \\ \hat{\beta}_1 &= \frac{\sum (Y_t - \bar{Y})(X_t - \bar{X})}{\sum (X_t - \bar{X})^2}. \end{align} \]

Where:

  • \(Y_t\) is the response at time \(t\).
  • \(X_t\) is the predictor at time \(t\).
  • \(\beta_0\) is the intercept.
  • \(\beta_1\) is the slope.
  • \(\varepsilon_t\) is the error term.

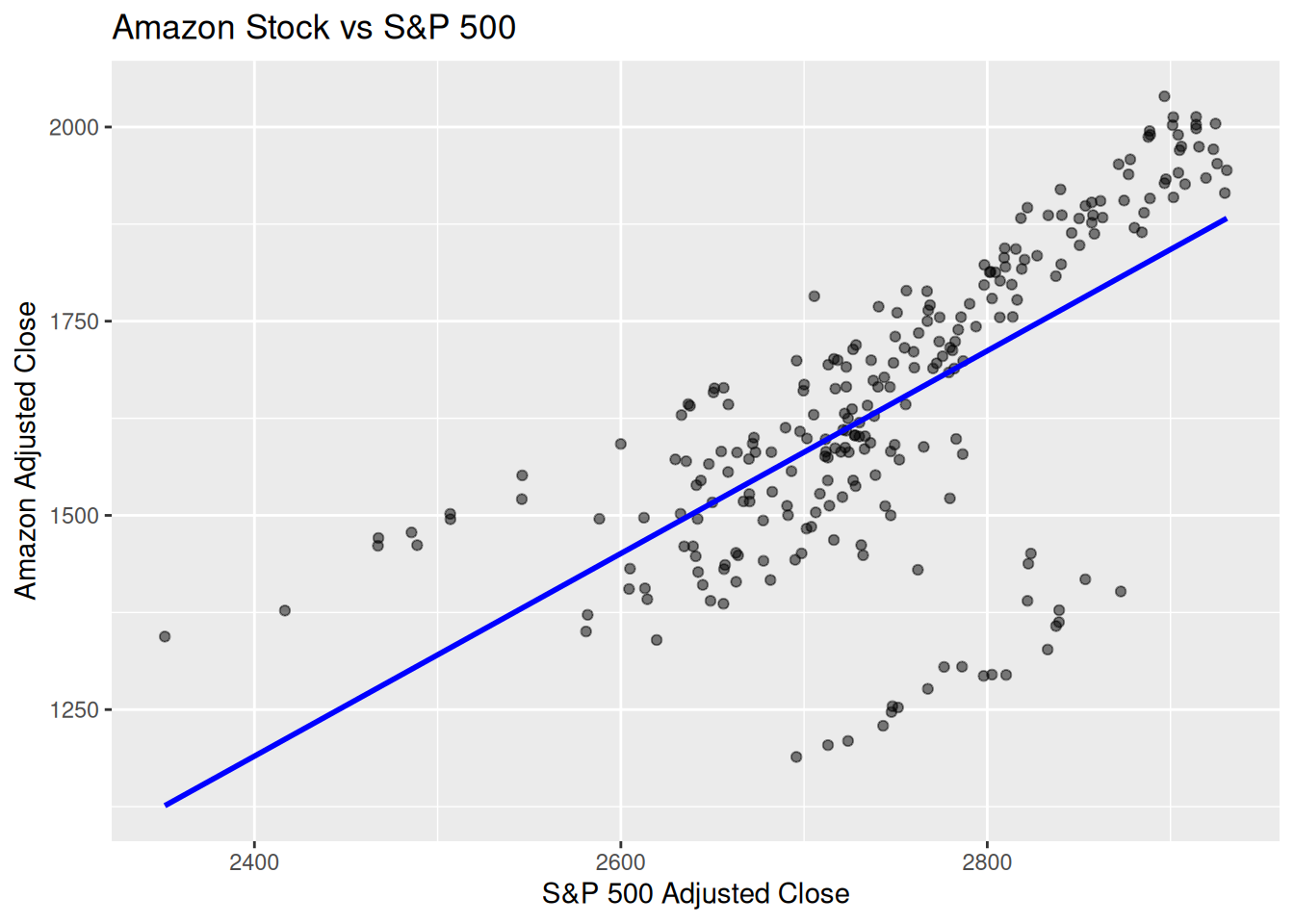
1.1 Finance Example (Amazon vs. S&P 500)

Dataset: gafa_stock (Amazon vs Market Index)

# 1) Get S&P 500 data (adjust as needed for start dates):
sp500 <- tq_get("^GSPC", from = "2018-01-01", to = "2019-12-31") %>%
  # Rename for consistency
  select(date, sp500_close = adjusted)

# 2) Use Amazon data from gafa_stock in fpp3:
amzn <- gafa_stock %>%
 filter(Symbol == "AMZN", Date >= "2018-01-01", Date <= "2018-12-31") %>%
 select(Date, amzn_close = Adj_Close)

# 3) Join by date
amzn_sp <- amzn %>%
  inner_join(sp500, by = c("Date" = "date")) 

# Regression coefficients
amzn_sp %>% 
  model(TSLM(amzn_close ~ sp500_close)) %>% 
  tidy() %>% 
  knitr::kable(caption = "Coefficients table")
Coefficients table
.model term estimate std.error statistic p.value
TSLM(amzn_close ~ sp500_close) (Intercept) -1940.961149 255.8360580 -7.586738 0
TSLM(amzn_close ~ sp500_close) sp500_close 1.304591 0.0930976 14.013160 0 
# 4) Quick visualization
 amzn_sp %>%
  ggplot(aes(x = sp500_close, y = amzn_close)) +
  geom_point(alpha = 0.5) +
  geom_smooth(method = "lm", se = FALSE, color = "blue") +
  labs(
    title = "Amazon Stock vs S&P 500",
    x = "S&P 500 Adjusted Close",
    y = "Amazon Adjusted Close"
  )

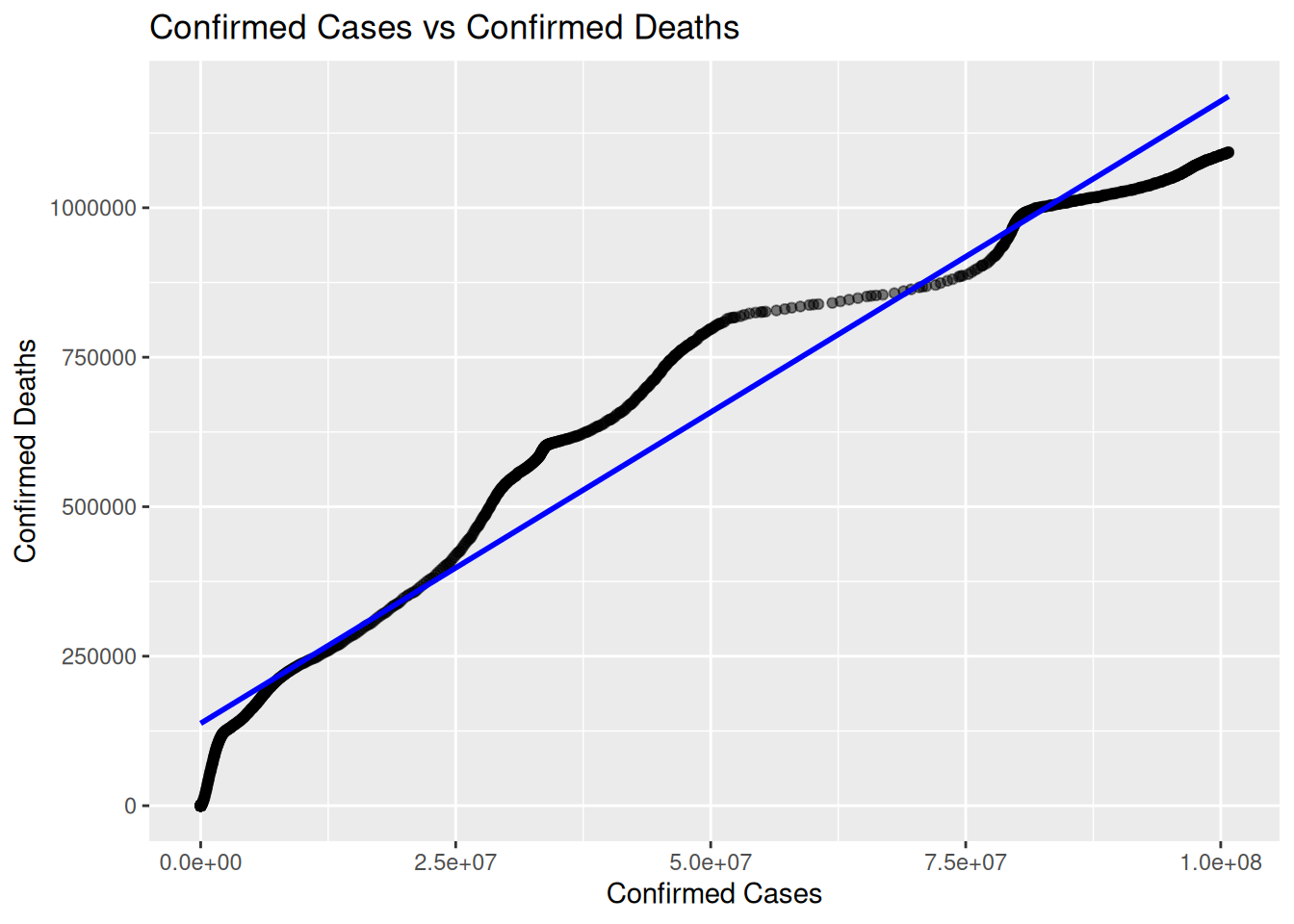
COVID Example (Mobility):

Dataset: oxcgrt (Oxford COVID Policy Tracker)

library(readr)
url <- "https://github.com/OxCGRT/covid-policy-dataset/raw/main/data/OxCGRT_compact_national_v1.csv"
oxcgrt <- read_csv(url)
  • Model: \(\log(\text{ConfirmedCases}_t) = \beta_0 + \beta_1\text{ConfirmedDeaths}_t + \varepsilon_t\)
  • Activity: Test \(H_0: \beta_1=0\) using \(t = \frac{\hat{\beta}_1}{SE(\hat{\beta}_1)}\)
oxcgrt %>% 
  filter(CountryName == "United States") %>% 
  mutate(Date = lubridate::ymd(Date)) %>% 
  as_tsibble(index = Date) %>% 
  tidyr::drop_na(ConfirmedCases,ConfirmedDeaths ) %>% 
  model(TSLM(ConfirmedCases ~ ConfirmedDeaths)) %>% 
  tidy()  %>% 
  knitr::kable(caption = "Coefficients table")
Coefficients table
.model term estimate std.error statistic p.value
TSLM(ConfirmedCases ~ ConfirmedDeaths) (Intercept) -1.054628e+07 4.288403e+05 -24.59255 0
TSLM(ConfirmedCases ~ ConfirmedDeaths) ConfirmedDeaths 9.148213e+01 6.202599e-01 147.48998 0 
oxdata <- oxcgrt %>% 
  filter(CountryName == "United States") %>% 
  mutate(Date = lubridate::ymd(Date)) %>% 
  as_tsibble(index = Date) 
  

oxdata %>% 
  ggplot(aes(x = ConfirmedCases, y = ConfirmedDeaths)) +
  geom_point(alpha = 0.5) +
  geom_smooth(method = "lm", se = FALSE, color = "blue") +
  labs(
    title = "Confirmed Cases vs Confirmed Deaths",
    x = "Confirmed Cases",
    y = "Confirmed Deaths"
  )

Using oxdata for further COVID anaysis

Lab Activity 1

  1. Filter the data to one country (e.g., ‘United States’).
  2. Create a new variable, log_cases, defined as \(\\(\log(1 + \text{ConfirmedCases})\\)\). (Adding 1 helps avoid \(\\(\log(0)\\).)\)
  3. Fit a TSLM model relating log_cases to C6M_Stay at home requirements.
  4. Interpret the slope coefficient.

Solution

# Filter & transform
exercise1_data <- oxcgrt %>%
  filter(CountryName == 'United States') %>%
  mutate(
    Date = ymd(Date),
    log_cases = log(1 + ConfirmedCases)
  ) %>%
  as_tsibble(index = Date) %>%
  drop_na(log_cases, `C6M_Stay at home requirements`)

# Fit TSLM
ex1_model <- exercise1_data %>%
  model(tslm_ex1 = TSLM(log_cases ~ `C6M_Stay at home requirements`))

# Summaries
ex1_model %>% tidy(tslm_ex1) %>% knitr::kable()
.model term estimate std.error statistic p.value
tslm_ex1 (Intercept) 14.976905 0.2302570 65.044305 0e+00
tslm_ex1 C6M_Stay at home requirements 0.917216 0.1722268 5.325628 1e-07 
ex1_model %>% glance(tslm_ex1) %>% knitr::kable()
.model r_squared adj_r_squared sigma2 statistic p_value df log_lik AIC AICc BIC CV deviance df.residual rank
tslm_ex1 0.0252702 0.0243792 15.75292 28.36231 1e-07 2 -3065.006 3025.699 3025.721 3040.697 15.81785 17233.7 1094 2

Lab Activity 2

  1. Filter to the same (or another) country.
  2. Define a new variable, log_deaths = \(\\(\log(1 + \text{ConfirmedDeaths})\\)\).
  3. Regress log_deaths on StringencyIndex_Average using TSLM.
  4. Check if increased stringency is correlated with reduced deaths (i.e., a negative slope).

Solution

# Filter & transform
exercise2_data <- oxcgrt %>%
  filter(CountryName == 'United States') %>%
  mutate(
    Date = ymd(Date),
    log_deaths = log(1 + ConfirmedDeaths)
  ) %>%
  as_tsibble(index = Date) %>%
  drop_na(log_deaths, StringencyIndex_Average)

# Fit TSLM
ex2_model <- exercise2_data %>%
  model(tslm_ex2 = TSLM(log_deaths ~ StringencyIndex_Average))

# Summaries
ex2_model %>% tidy(tslm_ex2)  %>% knitr::kable()
.model term estimate std.error statistic p.value
tslm_ex2 (Intercept) 9.3193169 0.2484414 37.51112 0
tslm_ex2 StringencyIndex_Average 0.0585671 0.0047442 12.34504 0 
ex2_model %>% glance(tslm_ex2)  %>% knitr::kable()
.model r_squared adj_r_squared sigma2 statistic p_value df log_lik AIC AICc BIC CV deviance df.residual rank
tslm_ex2 0.1222721 0.1214698 9.854598 152.3999 0 2 -2807.946 2511.578 2511.6 2526.577 9.911232 10780.93 1094 2