Activity34

Extending ETS Models with Predictors

Data Prep

• Use historical energy demand + temperature
  
• Ensure alignment in timestamps (drop_na())

energy_series <- vic_elec %>%
  filter_index(~ "2014-12-31") %>%
  dplyr::select(Time, Demand, Temperature) %>%
  drop_na()

Step 1 - Baseline ETS Model

# 1. ETS for Demand (non-seasonal)
demand_ets <- energy_series %>% model(ETS(Demand))
demand_ets_fc <- demand_ets %>% 
  forecast(h = "1 week") %>% 
  as_tibble() %>% 
  rename(mean = .mean) %>% 
  mutate(Model = "ETS")

\[\text{Demand}_t = \text{Level}_{t-1} + \text{Error}_t\]

The first model uses ETS (Error-Trend-Seasonal) for demand alone. This is limited because:

• Ignores temperature (known predictor)
• Assumes patterns are purely endogenous

Step 2 - ARIMAX with Temperature

# 2. ARIMAX with temperature forecasts
# First forecast temperature
temp_ets <- energy_series %>% model(ETS(Temperature))
temp_fc <- temp_ets %>% 
  forecast(h = "1 week") %>% 
  as_tibble() %>% 
  dplyr::select(Time, Temperature = .mean)

demand_dr <- energy_series %>% model(ARIMA(Demand ~ Temperature))

demand_dr_fc <- demand_dr %>% 
  forecast(new_data = temp_fc %>% as_tsibble(index = Time)) %>% 
  as_tibble() %>% 
  rename(mean = .mean) %>% 
  mutate(Model = "ARIMAX")

\[\text{Demand}_t = \phi_1 \text{Demand}_{t-1} + \beta \text{Temperature}_t + \epsilon_t\]

Improvement: Adds temperature as exogenous predictor.
But requires temperature forecasts - introduces error propagation if temperature predictions are poor.

---

Part 2: Why VAR Models Shine for Short-Term

Vector Autoregression (VAR)

\[\begin{cases} \text{Demand}_t = \alpha_1 + \sum_{i=1}^p \phi_{1i}\text{Demand}_{t-i} + \sum_{i=1}^p \psi_{1i}\text{Temp}_{t-i} \\ \text{Temp}_t = \alpha_2 + \sum_{i=1}^p \phi_{2i}\text{Demand}_{t-i} + \sum_{i=1}^p \psi_{2i}\text{Temp}_{t-i} \end{cases}\]

Key Advantages

1. Handles bidirectional relationships (temperature ↔︎ demand)
2. Captures lagged cross-effects
   
3. Better for short-term forecasts where system inertia matters

---

3. Critical Implementation Details

• Differencing: Makes series stationary for VAR (difference())
• Lag choice: 48 lags = 24hr periodicity (half-hourly data)
• Forecast alignment:

\[\text{VarForecast}_t = \text{LastObs} + \sum \text{DifferencedForecasts}_t\]

(Reverse the differencing through cumulative sums)

4. Comparison

• ETS: Good baseline but misses covariates
  
• ARIMAX: Better with good temp forecasts
  
• VAR: Best for short-term co-movements, no external forecast needed

# 3. VAR with tsDyn implementation
var_data <- energy_series %>% as_tibble() %>% 
  select(Demand, Temperature) %>%
  mutate(across(everything(), difference)) %>% 
  tidyr::drop_na()

var_model <- tsDyn::lineVar(var_data, lag = 48)
var_fc <- predict(var_model, n.ahead = 336)

# Align VAR forecasts with original scale
last_obs <- tail(energy_series, 1)
var_fc_demand <- tibble(
  Time = demand_ets_fc$Time,
  mean = last_obs$Demand + cumsum(var_fc[,1]),
  Model = "VAR"
)

# Combine forecasts 
combined_fc <- bind_rows(
  demand_ets_fc %>% select(Time, Model, mean),
  demand_dr_fc %>% select(Time, Model, mean),
  var_fc_demand
)

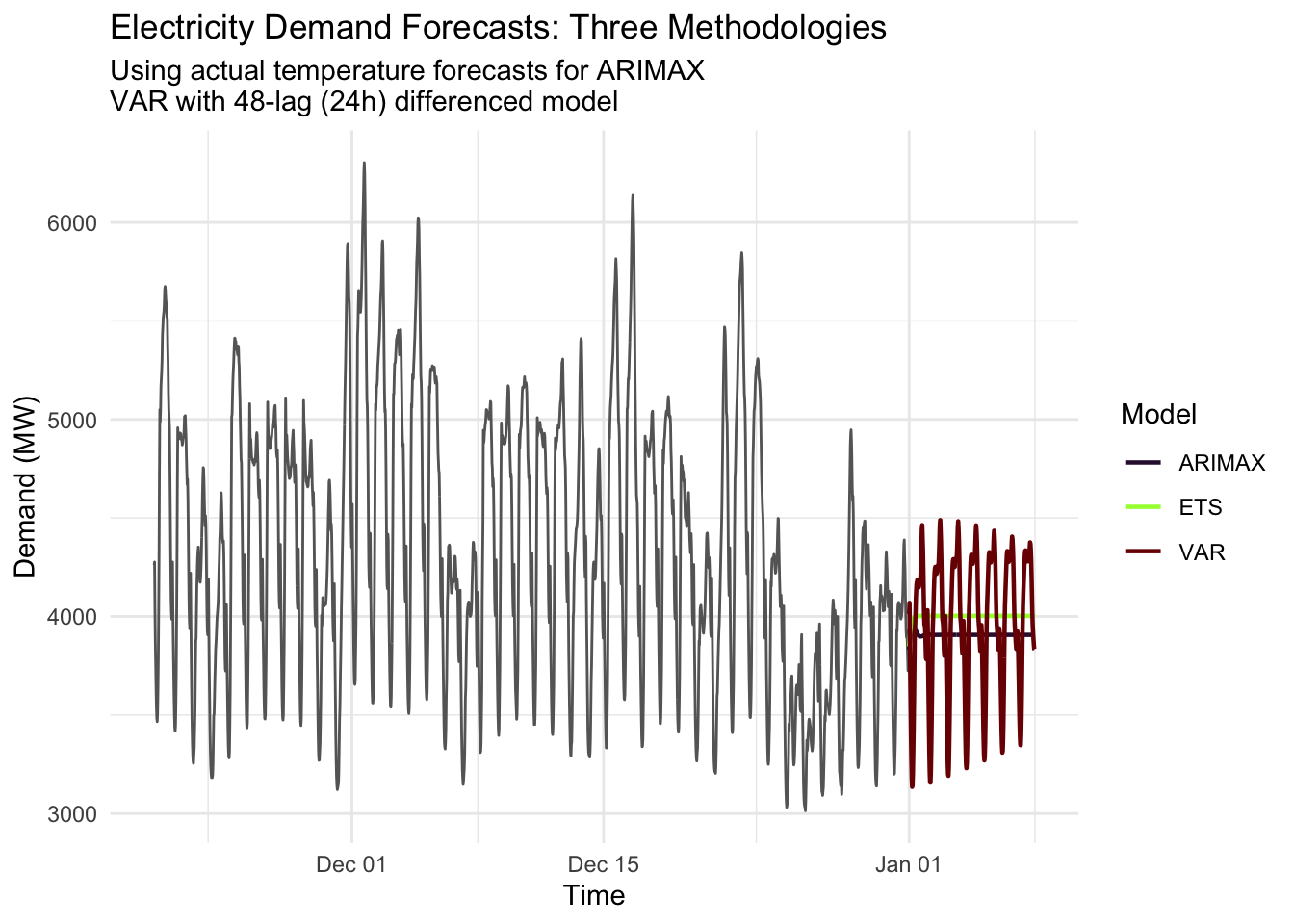
# Plot with accurate comparisons
ggplot() +
  geom_line(data = energy_series %>% tail(2016),  # Last 2 weeks
           aes(x = Time, y = Demand), color = "gray40") +
  geom_line(data = combined_fc, 
           aes(x = Time, y = mean, color = Model), linewidth = 0.8) +
  labs(title = "Electricity Demand Forecasts: Three Methodologies",
       subtitle = "Using actual temperature forecasts for ARIMAX\nVAR with 48-lag (24h) differenced model",
       y = "Demand (MW)") +
  theme_minimal() +
  scale_color_viridis_d(option = "H")