Activity23

1. SARIMA Model Structure

A SARIMA\((p,d,q)(P,D,Q)_m\) model combines:

Regular components: AR(p), MA(q) terms for short-term patterns
Seasonal components: Seasonal AR(P), MA(Q) terms at period \(m\)
Differencing: \(d\) regular differences + \(D\) seasonal differences

2. Strategic Differencing

Key Principle: Use minimal differencing to stabilize mean/variance

# AirPassengers dataset
ap_ts <- tsibble::as_tsibble(AirPassengers) %>% 
  index_by(Date = yearmonth(index)) %>% 
  rename(Passengers = value)

# Automated selection
ap_ts %>% 
  features(Passengers, list(unitroot_kpss, unitroot_ndiffs, unitroot_nsdiffs))

# A tibble: 1 × 4
  kpss_stat kpss_pvalue ndiffs nsdiffs
      <dbl>       <dbl>  <int>   <int>
1      2.98        0.01      1       0

# Visual check
ap_ts %>%
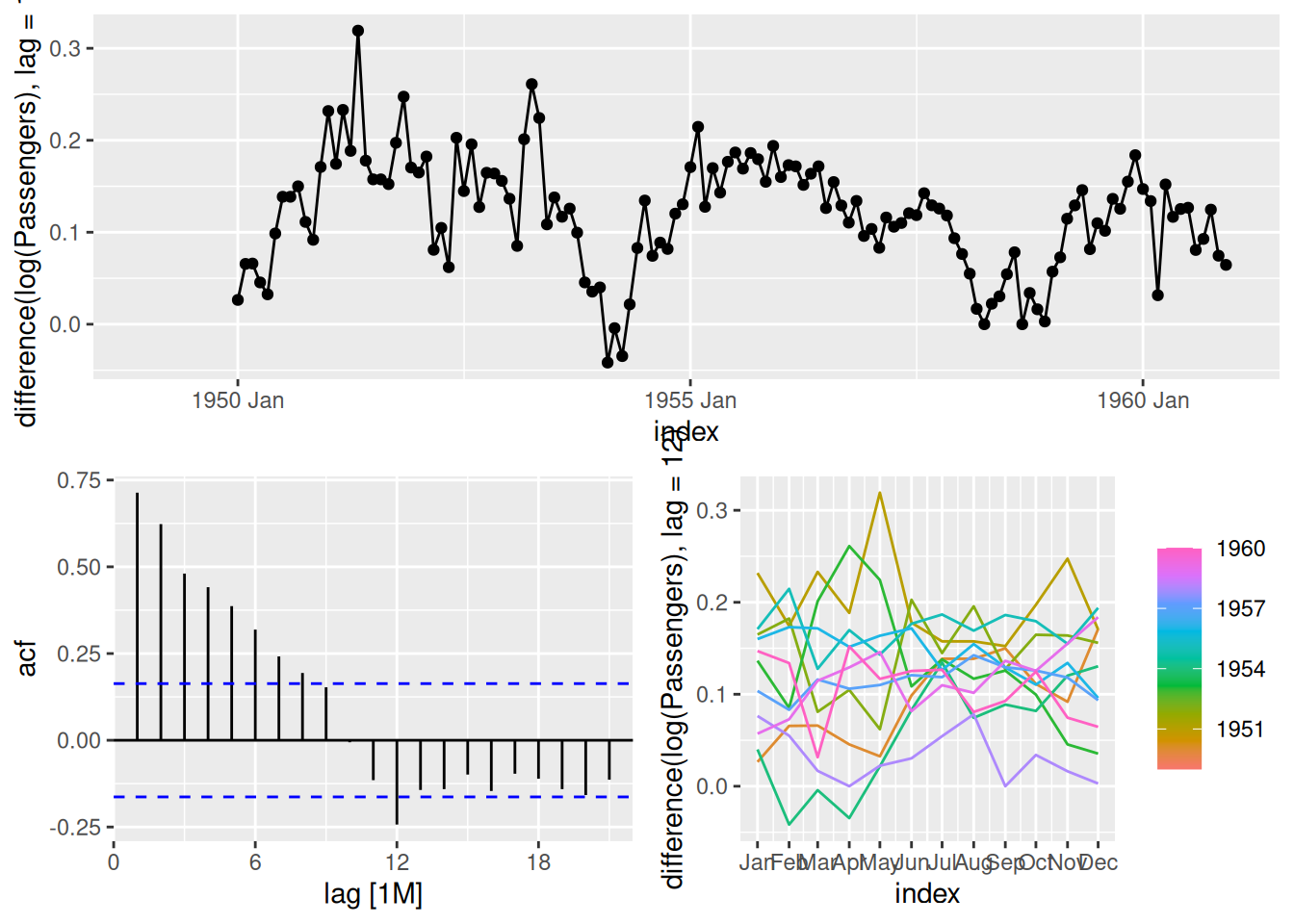
  gg_tsdisplay(difference(log(Passengers), lag = 12))

Insight: Seasonal differencing (lag=12) removes yearly patterns while preserving monthly trends

3. Model Building

3.1 Candidate Models

models <- ap_ts %>%
  model(
    Auto = ARIMA(log(Passengers)),
    Manual1 = ARIMA(log(Passengers) ~ pdq(1,1,1) + PDQ(0,1,1, period=12)),
    Manual2 = ARIMA(log(Passengers) ~ pdq(2,1,0) + PDQ(1,1,0, period=12))
  )

glance(models) %>% arrange(AICc)

# A tibble: 3 × 8
  .model   sigma2 log_lik   AIC  AICc   BIC ar_roots   ma_roots  
  <chr>     <dbl>   <dbl> <dbl> <dbl> <dbl> <list>     <list>    
1 Auto    0.00132    250. -489. -489. -475. <cpl [2]>  <cpl [12]>
2 Manual1 0.00137    245. -482. -482. -470. <cpl [1]>  <cpl [13]>
3 Manual2 0.00148    241. -474. -473. -462. <cpl [14]> <cpl [0]>

3.2 Coefficient Check

For top model:

final_model <- models %>% 
  select(Auto)

tidy(models) %>% 
  filter(.model == "Auto")

# A tibble: 4 × 6
  .model term     estimate std.error statistic  p.value
  <chr>  <chr>       <dbl>     <dbl>     <dbl>    <dbl>
1 Auto   ar1        0.575    0.0843       6.83 2.83e-10
2 Auto   ar2        0.261    0.0842       3.11 2.33e- 3
3 Auto   sma1      -0.555    0.0771      -7.21 3.99e-11
4 Auto   constant   0.0193   0.00149     13.0  2.07e-25

4. Model Refinement Cycle

Start with automatic differencing
Compare multiple model specifications
Validate residuals systematically
Iterate using PACF patterns

# Final refinement example
ap_ts %>%
  model(
    Best = ARIMA(log(Passengers) ~ pdq(1,1,1) + PDQ(0,1,1, period=12))
  ) %>% 
  report()

Series: Passengers 
Model: ARIMA(1,1,1)(0,1,1)[12] 
Transformation: log(Passengers) 

Coefficients:
         ar1      ma1     sma1
      0.1960  -0.5784  -0.5643
s.e.  0.2475   0.2132   0.0747

sigma^2 estimated as 0.001375:  log likelihood=244.95
AIC=-481.9   AICc=-481.58   BIC=-470.4

Lab Activity

1. Data Preparation

Q1: Examine the seasonal patterns using gg_season(). What type of seasonality dominates this series?

2. Model Specification

Fit SARIMA(1,1,1)(0,1,1)₁₂ model with maximum likelihood estimation

Q2: Interpret the model structure:

What does the (1,1,1) non-seasonal component represent?
Why do we use PDQ(0,1,1) for seasonal terms?

3. Parameter Estimation

Task: Extract and interpret coefficients

Q3: Which coefficients are statistically significant (α=0.05)? What does the MA(1) coefficient suggest?

4. Residual Diagnostics

4.1 Visual Analysis

Q4: Do residuals show concerning autocorrelation patterns? Justify your answer.

4.2 Formal Tests

Q5: Interpret the Ljung-Box (LB) test results:

Can we maintain the white noise assumption?

5. Model Validation

Task: Check specification robustness

Q6: Compare AICc values across estimation methods. Does our original model remain preferred?