Activity44

VAR Modeling and Forecast

Let’s model weekly COVID-19 trajectories using logged differenced time series (\(\Delta y_t = \log(y_t - y_{t-1} + 1)\)) to stabilize variance.

library(COVID19)
# Retrieve COVID-19 data for the United States and prepare a tsibble
covid_raw <- covid19(country = "US", level = 1, verbose = FALSE) %>%
  as_tsibble(index = date) %>%
  select(date, confirmed, deaths, people_vaccinated) %>%
  rename(vaccines = people_vaccinated)

# Convert to NEW weekly cases 
covid_weekly <- covid_raw %>%
  mutate(across(c(confirmed, deaths, vaccines), ~. - lag(.))) %>% 
  index_by(week = yearweek(date)) %>%
  summarize(
    cases = sum(confirmed, na.rm = TRUE),
    deaths = sum(deaths, na.rm = TRUE),
    vaccines = sum(vaccines, na.rm = TRUE)
  ) %>%
  filter(cases > 0, deaths > 0, vaccines >= 0) %>%
  mutate(across(c(cases, deaths, vaccines), ~ log(. + 1))) 

bp_cases <- breakpoints(cases ~ 1 + vaccines + deaths, data = covid_weekly, h = 0.2)
break_dates <- covid_weekly$week[bp_cases$breakpoints]

# Create regime dummy
covid_weekly <- covid_weekly %>%
  mutate(
    intervention_period = case_when(
      week < break_dates[1] ~ "pre",
      week >= break_dates[1] & week < break_dates[2] ~ "phase1",
      week >= break_dates[2] & week < break_dates[3] ~ "phase2",
      week >= break_dates[3] ~ "post"
    )
  )

n_total <- nrow(covid_weekly)
h <- round(0.2 * n_total)
train <- covid_weekly[1:(n_total - h), ]
test <- covid_weekly[(n_total - h + 1):n_total, ]

# Initialize forecast storage
forecast_df <- tibble(
  week = test$week,
  actual_cases = exp(test$cases) - 1,
  actual_deaths = exp(test$deaths) - 1,
  actual_vaccines = exp(test$vaccines) - 1
)

Model Specifications

Benchmark: Fit a univariate ARIMA model to weekly cases using automated order selection
ARIMAX: Extend ARIMA with vaccines as exogenous regressor (\(\text{cases}_t \sim \text{vaccines}_t\))
VAR(2): Model bidirectional relationships between cases and vaccines with 2-lag structure:
\(Y_t = \begin{bmatrix}\text{cases}_t\\ \text{vaccines}_t\end{bmatrix} = A_1Y_{t-1} + A_2Y_{t-2} + \epsilon_t\)
VAR(3): Tri-variate system incorporating deaths with 3-lag structure
ETS: Automated exponential smoothing state-space model

# Model 1: Univariate ARIMA
fit_arima <- train %>%
  model(ARIMA(cases))

fc_arima <- forecast(fit_arima, h = h) %>%
  mutate(arima_cases = exp(.mean) - 1)

# Model 2: ARIMAX with Vaccines
fit_arimax <- train %>%
  model(ARIMA(cases ~ vaccines))

fc_arimax <- forecast(fit_arimax, new_data = test) %>%
  mutate(arimax_cases = exp(.mean) - 1)

# Model 3: VAR(2) - Cases & Vaccines
var2_data <- train %>% as_tibble() %>% 
  select(cases, vaccines) %>%
  mutate(across(everything(), difference)) %>%
  drop_na()

var2_model <- VAR(var2_data, p = 2)
fc_var2 <- predict(var2_model, n.ahead = h)

last_val_cases <- tail(train$cases, 1)
var2_fc_cases <- cumsum(fc_var2$fcst$cases[,1]) + last_val_cases
forecast_df$var2_cases <- exp(var2_fc_cases) - 1

last_val_vaccines <- tail(train$vaccines, 1)
var2_fc_vaccines <- cumsum(fc_var2$fcst$vaccines[,1]) + last_val_vaccines
forecast_df$var2_vaccines <- exp(var2_fc_vaccines) - 1

# Model 4: VAR(3) - Cases, Deaths, Vaccines
var3_data <- train %>% as_tibble() %>% 
  select(cases, deaths, vaccines) %>%
  mutate(across(everything(), difference)) %>%
  drop_na()

var3_model <- VAR(var3_data, p = 3)
fc_var3 <- predict(var3_model, n.ahead = h)


last_val_cases <- tail(train$cases, 1)
var3_fc_cases <- cumsum(fc_var3$fcst$cases[,1]) + last_val_cases
forecast_df$var3_cases <- exp(var3_fc_cases) - 1

last_val_vaccines <- tail(train$vaccines, 1)
var3_fc_vaccines <- cumsum(fc_var3$fcst$vaccines[,1]) + last_val_vaccines
forecast_df$var3_vaccines <- exp(var3_fc_vaccines) - 1

last_val_deaths <- tail(train$deaths, 1)
var3_fc_deaths <- cumsum(fc_var3$fcst$deaths[,1]) + last_val_deaths
forecast_df$var3_deaths <- exp(var3_fc_deaths) - 1

# Model 5: ETS 
fit_ets <- train %>%
  model(ETS(cases))

fc_ets <- forecast(fit_ets, h = h) %>%
  mutate(ets_cases = exp(.mean) - 1)

library(Metrics)
library(MLmetrics)
# Accuracy Metrics Calculation
metrics <- tibble(
  Model = c("ARIMA", "ARIMAX", "VAR(2)", "VAR(3)", "ETS"),
  MAE = c(
    mae(forecast_df$actual_cases, fc_arima$arima_cases),
    mae(forecast_df$actual_cases, fc_arimax$arimax_cases),
    mae(forecast_df$actual_cases, forecast_df$var2_cases),
    mae(forecast_df$actual_cases, forecast_df$var3_cases),
    mae(forecast_df$actual_cases, fc_ets$ets_cases)
  ),
  MAPE = c(
    mape(forecast_df$actual_cases, fc_arima$arima_cases),
    mape(forecast_df$actual_cases, fc_arimax$arimax_cases),
    mape(forecast_df$actual_cases, forecast_df$var2_cases),
    mape(forecast_df$actual_cases, forecast_df$var3_cases),
    mape(forecast_df$actual_cases, fc_ets$ets_cases) 
    
  ),
  RMSE = c(
    rmse(forecast_df$actual_cases, fc_arima$arima_cases),
    rmse(forecast_df$actual_cases, fc_arimax$arimax_cases),
    rmse(forecast_df$actual_cases, forecast_df$var2_cases),
    rmse(forecast_df$actual_cases, forecast_df$var3_cases),
    rmse(forecast_df$actual_cases, fc_ets$ets_cases) 
  ),
   Bias = c(
    mean(fc_arima$arima_cases - forecast_df$actual_cases),
    mean(fc_arimax$arimax_cases - forecast_df$actual_cases),
    mean(forecast_df$var2_cases - forecast_df$actual_cases),
    mean(forecast_df$var3_cases - forecast_df$actual_cases),
    mean(fc_ets$ets_cases - forecast_df$actual_cases)
  ),
  R2 = c(
    R2_Score(fc_arima$arima_cases, forecast_df$actual_cases),
    R2_Score(fc_arimax$arimax_cases, forecast_df$actual_cases),
    R2_Score(forecast_df$var2_cases, forecast_df$actual_cases),
    R2_Score(forecast_df$var3_cases, forecast_df$actual_cases),
    R2_Score(fc_ets$ets_cases, forecast_df$actual_cases)
  )
)
metrics %>%  knitr::kable()

Model	MAE	MAPE	RMSE	Bias	R2
ARIMA	181316.8	0.7059227	211070.5	169885.8	-1.7278961
ARIMAX	136716.9	0.3821726	164800.2	-133689.6	-0.6629847
VAR(2)	182251.2	0.7037307	207695.5	180974.8	-1.6413571
VAR(3)	317627.4	1.2251102	365140.8	313386.1	-7.1638232
ETS	172758.6	0.5315084	218620.2	-171756.7	-1.9265338

# Visualization
ggplot(forecast_df, aes(x = week)) +
  geom_line(aes(y = actual_cases, color = "Actual"), size = 1) +          # Map to "Actual"
  geom_line(aes(y = var2_cases, color = "VAR2")) +                        # Map to "VAR2"
  geom_line(aes(y = var3_cases, color = "VAR3")) +                        # Map to "VAR3"
  geom_line(data = fc_ets, aes(y = ets_cases, color = "ETS")) +           # Map to "ETS"
  geom_line(data = fc_arima, aes(y = arima_cases, color = "ARIMA")) +     # Map to "ARIMA"
  geom_line(data = fc_arimax, aes(y = arimax_cases, color = "ARIMAX")) +  # Map to "ARIMAX"
  labs(
    title = "Model Forecast Comparison - Weekly COVID Cases",
    subtitle = "Colors represent models", 
    y = "Cases",
    color = "Model" 
  ) +
  scale_color_manual(
    values = c(
      "Actual" = "black",
      "VAR2" = "#E69F00",  
      "VAR3" = "#56B4E9",  
      "ETS" = "#009E73",   
      "ARIMA" = "#CC79A7", 
      "ARIMAX" = "#0072B2" 
    )
  ) +
  theme_minimal() +
  theme(legend.position = "bottom")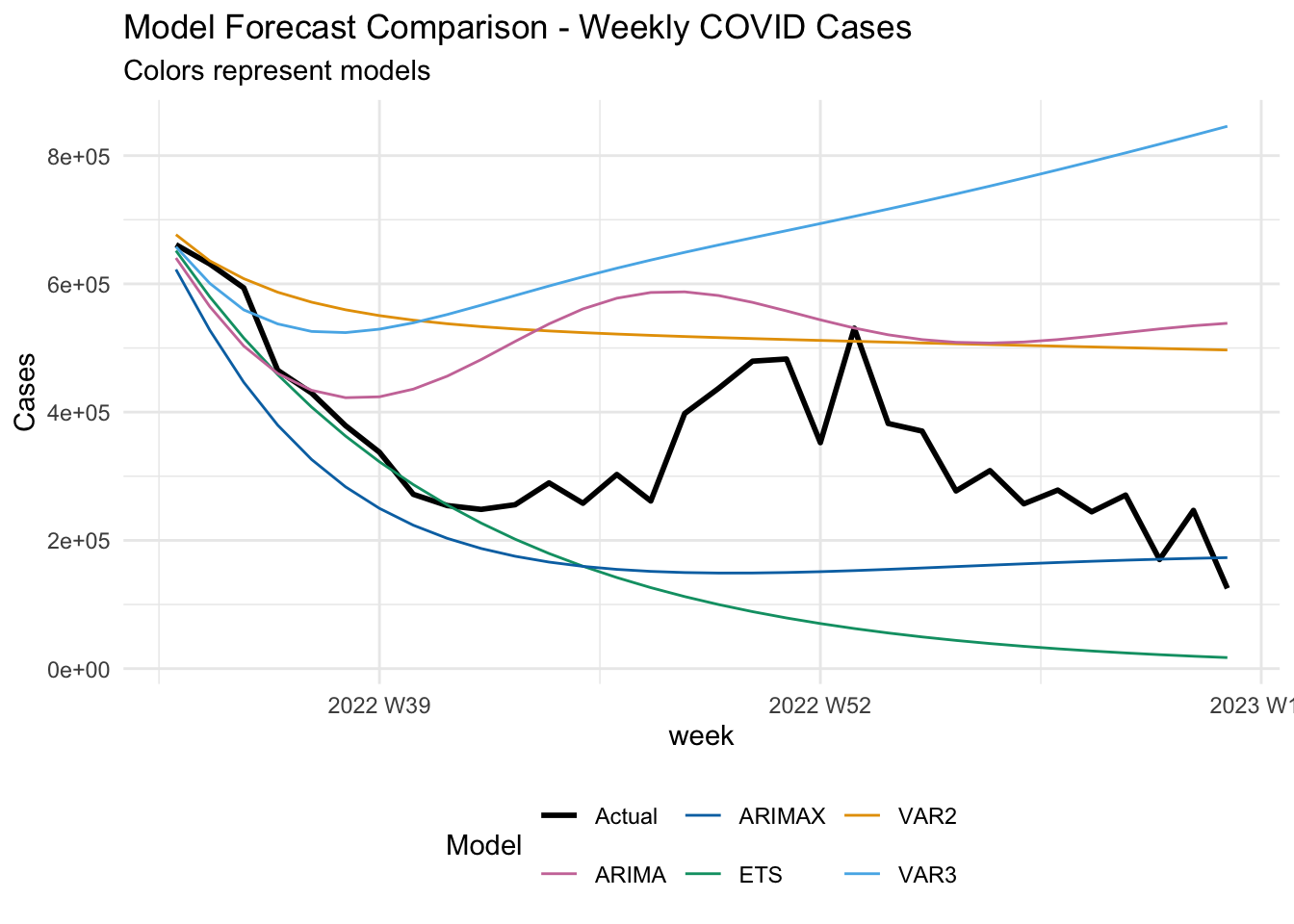

Conceptual Discussion Questions

Q1: Why difference the series before VAR estimation?

Q2: What advantage does VAR have over ARIMAX for policy analysis?

Q3: What diagnostic checks would you perform to assess VAR model stability, and why might differencing alone be insufficient?

Q4: When would you prefer ETS/ARIMA over VAR despite their lower forecast accuracy in this study?

Q5: Why might automated ARIMA selection fail to detect regime-dependent dynamics?