Activity21
Theoretical Foundations of AR Models
Time Series Nature & Stationarity
Define AR(\(p\)): \(Y_t = \phi_1 Y_{t-1} + \dots + \phi_p Y_{t-p} + \epsilon_t\), \(\epsilon_t \sim WN(0,\sigma^2)\)
AR(p) Properties:
- Captures temporal dependence through lagged terms
- PACF cuts off after lag \(p\)
- Requires stationarity for reliable inference
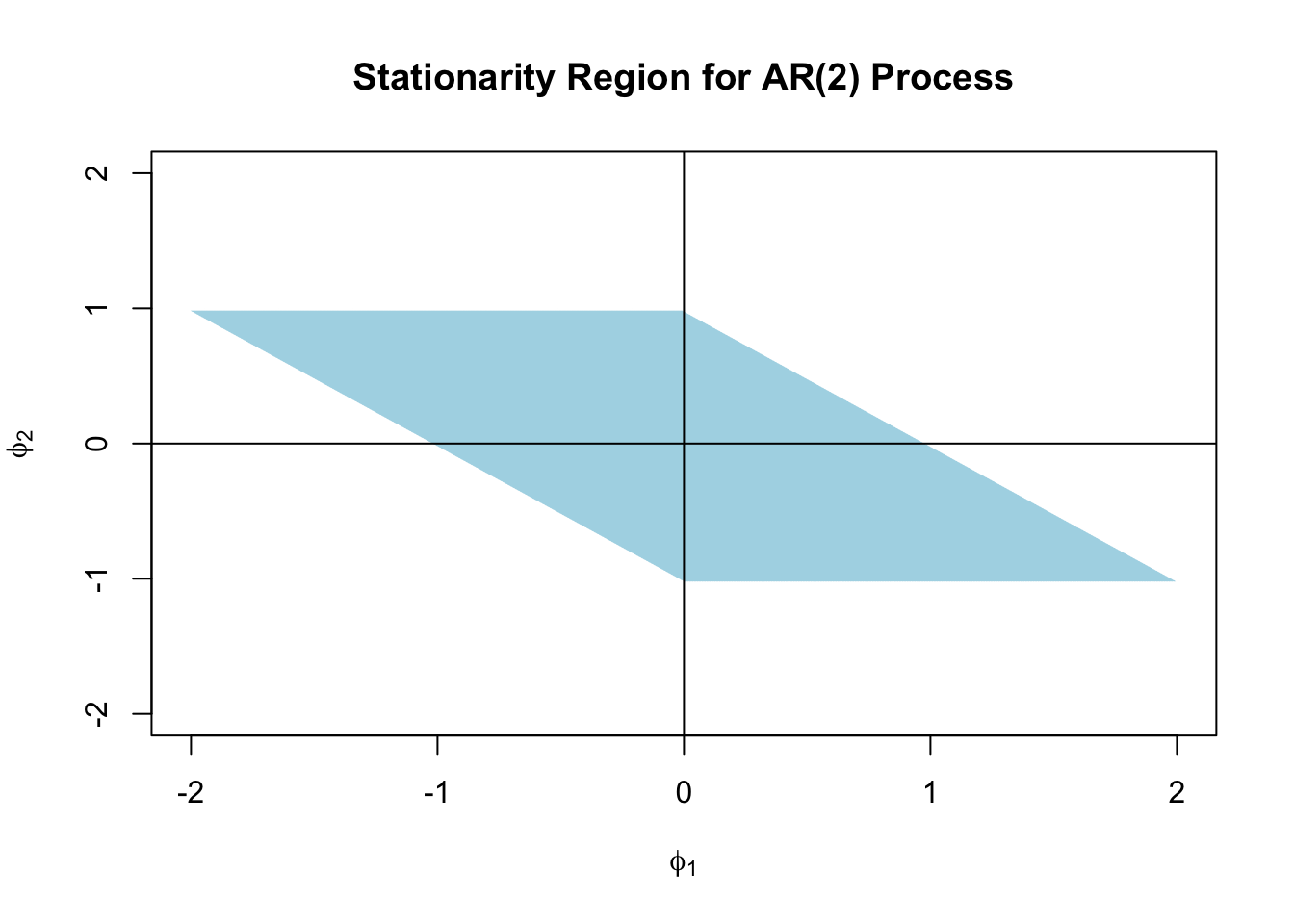
- Unit root non-stationarity occurs when characteristic equation \(1 - \phi_1 z - \cdots - \phi_p z^p = 0\) has roots on unit circle
library(fable)
set.seed(123)
ar_data <- tibble(time = 1:100, y = arima.sim(model = list(ar = c(0.7, -0.2)), n = 100)) %>%
as_tsibble(index = time)
ar_data %>%
gg_tsdisplay(y, plot_type = c("scatter")) + # ACF/PACF
labs(title = "AR(2) Process: φ₁=0.7, φ₂=-0.2")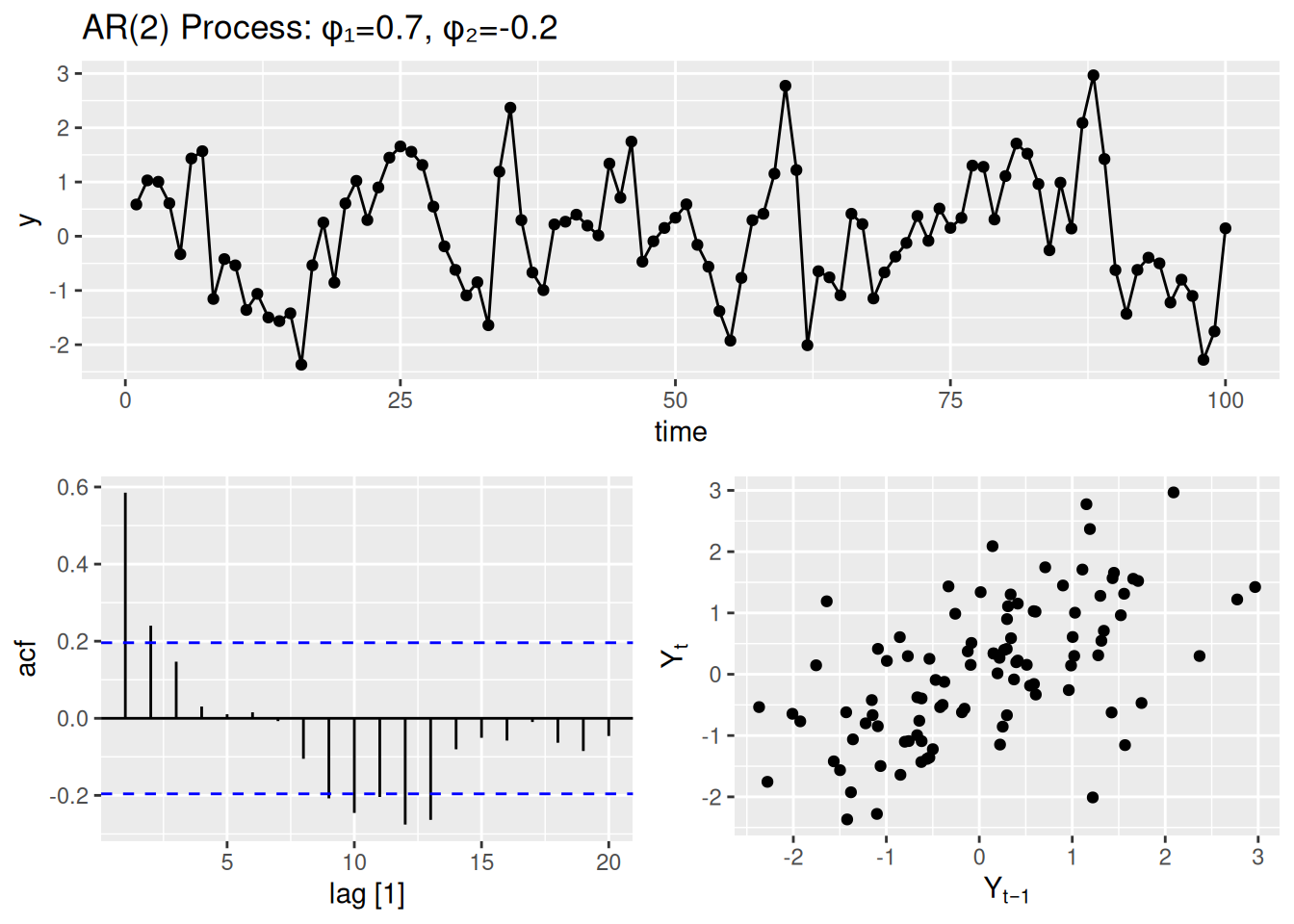
Model Fitting & Diagnostics
fit_ar <- ar_data %>%
model(ARIMA(y ~ pdq(2,0,0))) # Explicit AR specification
report(fit_ar) # Check coefficients & σ²Series: y
Model: ARIMA(2,0,0)
Coefficients:
ar1 ar2
0.6757 -0.1576
s.e. 0.0990 0.1002
sigma^2 estimated as 0.8167: log likelihood=-130.99
AIC=267.99 AICc=268.24 BIC=275.8fit_ar %>% residuals() %>% gg_tsdisplay(plot_type = c("scatter")) # Residual diagnostics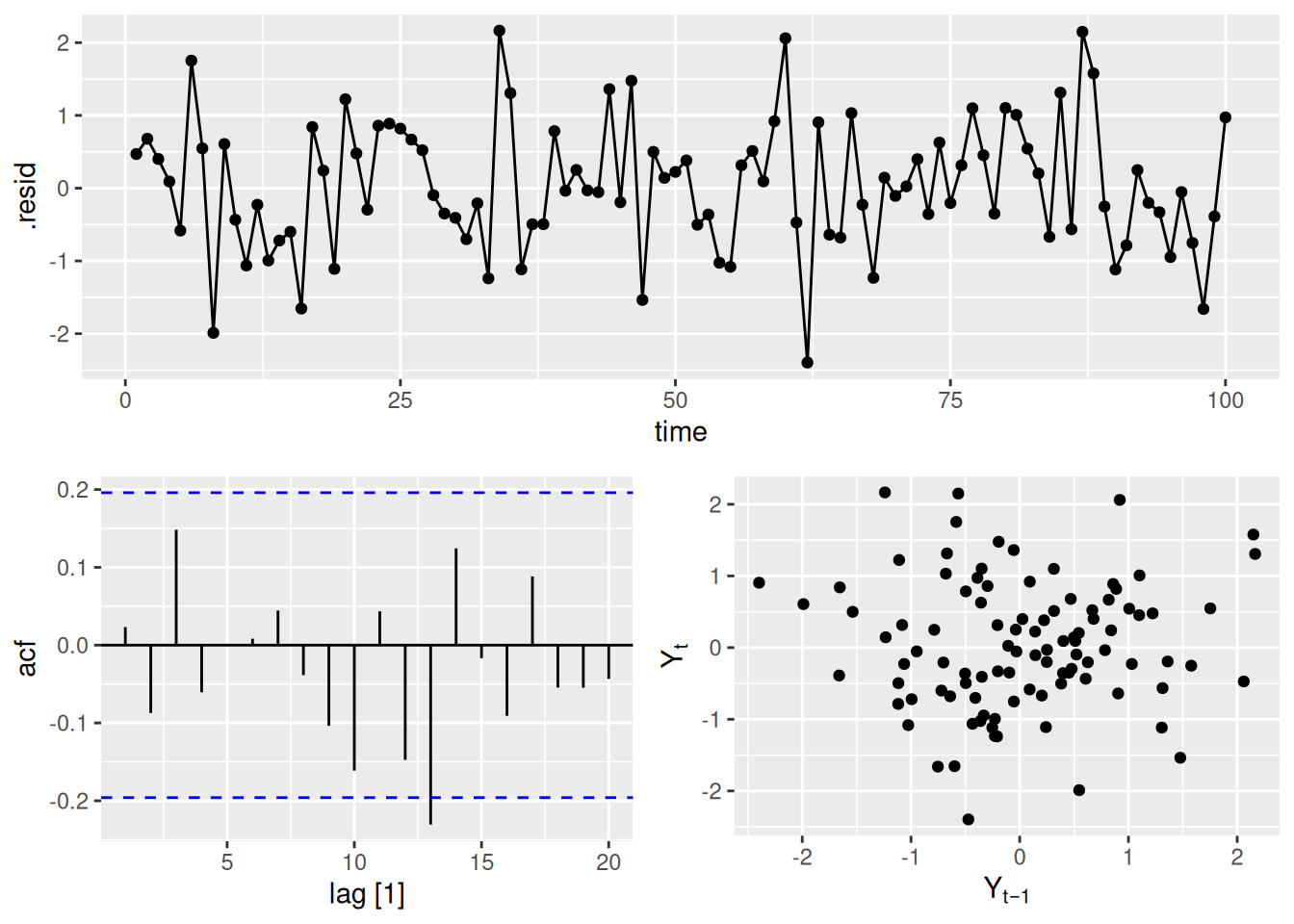
Real-World Process: US Consumption
From the global_economy dataset (Ch. 5 of text), we’ll analyze quarterly percentage changes in personal consumption expenditures (stationary series):
Lab Activity A: AR Modeling with Real Data
Exploratory Analysis & Stationarity
- Visualize Series:
- Stationarity Assessment:
Model Fitting & Forecasting
- Fit AR Model:
- Residual Diagnostics:
- Forecasting:
Lab Activity B: Real-World Application - US Income Changes
1. Data Preparation & Visualization
2. Order Identification
Determine appropriate AR order through PACF:
3. Model Comparison
Fit competing specifications and evaluate:
4. Forecasting & Policy Implications
Using the best model, generate forecasts up-to 10 time points into the future and interpret economic meaning: