Activity24

Theoretical Background: Volatility Clustering

Volatility clustering (periods of high/low variability persisting) violates ARIMA’s constant variance assumption. Common in COVID-19 cases (waves) and stock returns (crashes). ARCH (Autoregressive Conditional Heteroskedasticity) tests help detect this phenomenon.

Mathematical Foundation

  • ARCH Model:

    The ARCH(q) model for volatility is defined as:
    \[ \begin{align*} r_t &= \mu_t + \epsilon_t, \quad \epsilon_t = \sigma_t z_t, \\ \sigma_t^2 &= \alpha_0 + \alpha_1 \epsilon_{t-1}^2 + \dots + \alpha_q \epsilon_{t-q}^2 \end{align*} \]
    where \(z_t \sim N(0,1)\), and \(\alpha_0 > 0\), \(\alpha_i \geq 0\).

  • Key Idea:

    Variance \(\sigma_t^2\) depends on past squared residuals (\(\epsilon_{t-1}^2, \dots, \epsilon_{t-q}^2\)), capturing volatility clustering.

Testing Steps

  1. Fit ARIMA Model:
    Model the mean structure (e.g., log returns).

  2. Extract Residuals:
    Compute residuals \(\epsilon_t\) and squared residuals \(\epsilon_t^2\).

  3. Visual Diagnostics:

    • Plot ACF/PACF of squared residuals.
    • Look for significant autocorrelation (sign of ARCH effects).

  4. Statistical Tests:

    • Ljung-Box Test: Tests autocorrelation in \(\epsilon_t^2\).
    • Engle’s ARCH Test: Formal Lagrange Multiplier (LM) test for ARCH effects.

Example 1: COVID-19 Cases

Data Preparation

Use the COVID19 package to fetch daily confirmed cases in Italy (clear volatility during waves):

library(COVID19)
library(fpp3)

# Get data
covid_data <- covid19(country = "Italy", level = 1, verbose = FALSE) %>%
  as_tsibble(index = date) %>%
  mutate(new_cases = difference(confirmed)) %>%
  mutate(log_new_cases = difference(log(confirmed))) %>%
  drop_na(log_new_cases, new_cases) %>% 
  mutate(scaled_cases = scale(log_new_cases))

Model Fitting & Volatility Check

Fit an ARIMA model to new_cases and inspect residuals:

fit_covid <- covid_data %>%
  model(ARIMA(scaled_cases ~ pdq(2,1,1) + PDQ(0,0,0)))

# Check residuals for volatility clustering
fit_covid %>% gg_tsresiduals()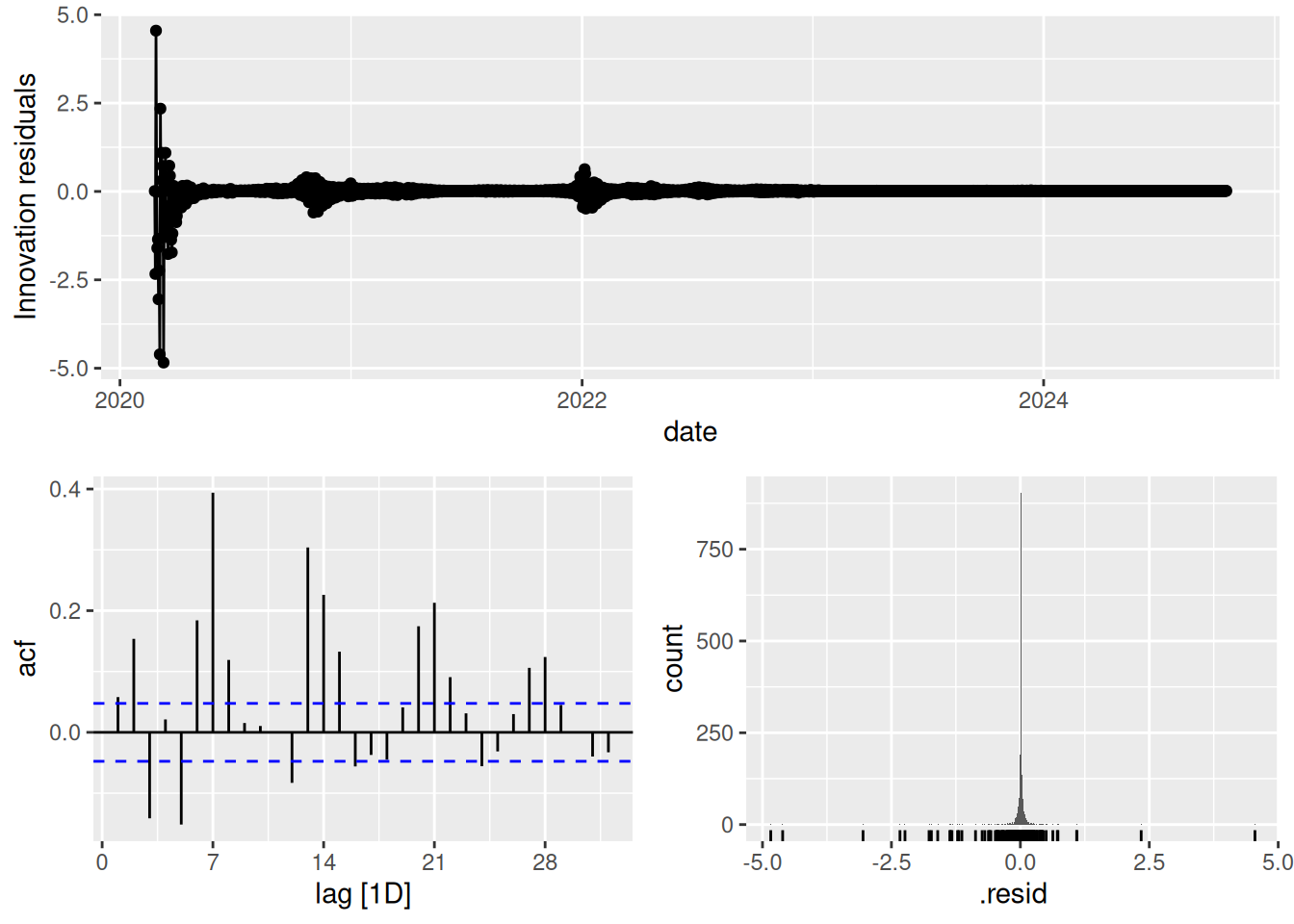

augment(fit_covid) %>%
  ggplot(aes(x = date, y = .resid^2)) +
  geom_line() + labs(title = "Squared Residuals (COVID-19 Cases)")

fit_covid %>% 
  augment() %>% 
  features(.innov,~ljung_box(.x, lag=24, dof=4)
  )
# A tibble: 1 × 3
  .model                                            lb_stat lb_pvalue
  <chr>                                               <dbl>     <dbl>
1 ARIMA(scaled_cases ~ pdq(2, 1, 1) + PDQ(0, 0, 0))    920.         0

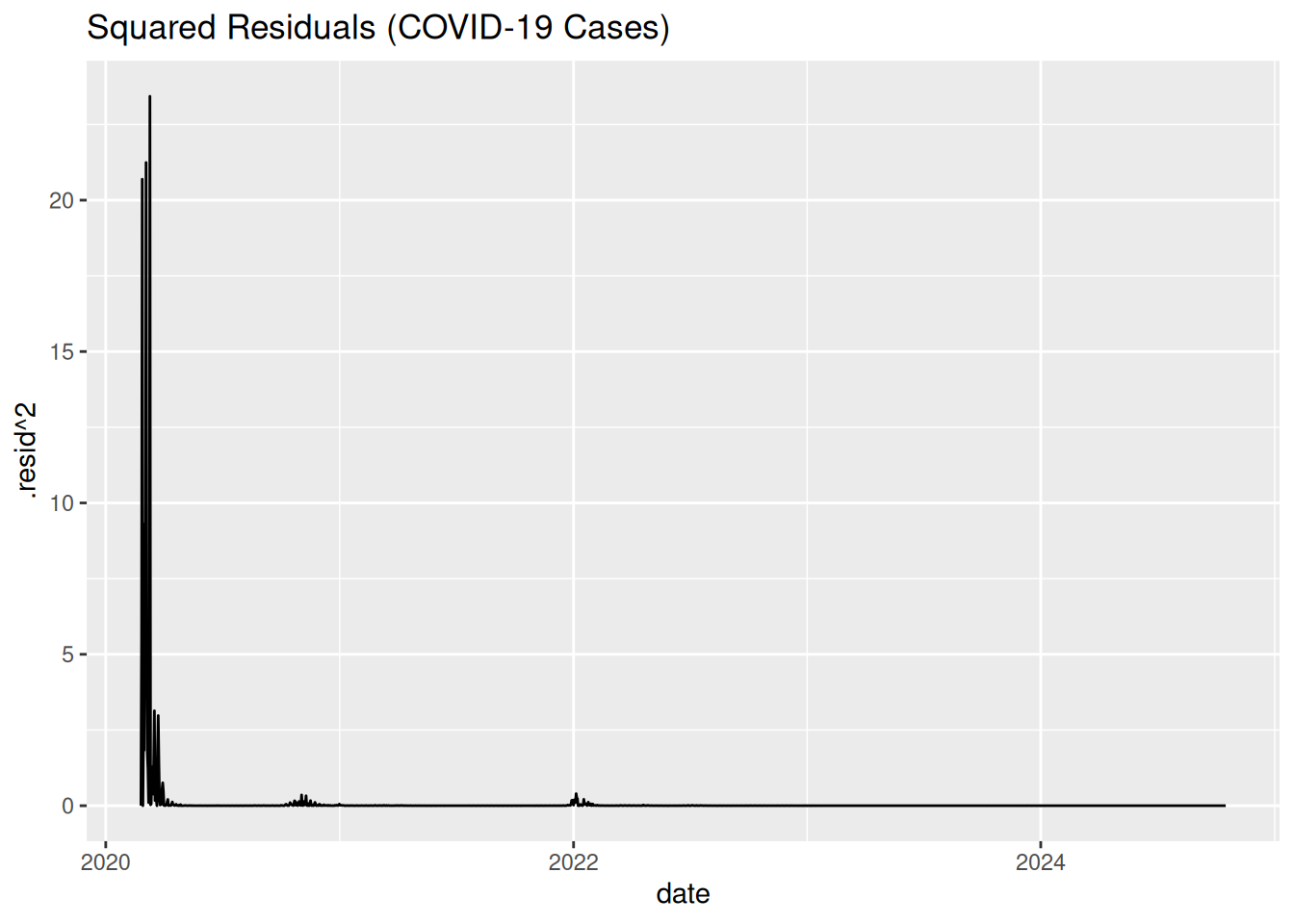
Key Observation: Squared residuals cluster many times between January 2020 and January 2023 (COVID waves), indicating volatility clustering.

augment(fit_covid) %>%
  ggplot(aes(x = date, y = .resid^2)) +
  geom_line() + labs(title = "Squared Residuals (COVID-19 Cases)")

Example 2: Stock Returns

Data Preparation

Fetch S&P 500 returns using tq_get() (more realistic volatility with irregular trading days):

# Get S&P 500 data and calculate daily returns
sp500 <- tq_get("^GSPC", get = "stock.prices", from = "2000-01-01") %>%
  as_tsibble(index = date) %>%  
  fill_gaps() %>% 
  fill(close, .direction = "down") %>% 
  mutate(return = difference(log(close))) %>%  
  drop_na(return)

Model Fitting & Volatility Check

fit_sp500 <- sp500 %>%
  model(ARIMA(return ~ pdq(1,0,1)))  

# Visualize squared residuals for volatility clustering
augment(fit_sp500) %>%
  ggplot(aes(x = date, y = .resid^2)) +
  geom_line(alpha = 0.6) +
  labs(title = "Squared Residuals (S&P 500 Returns)")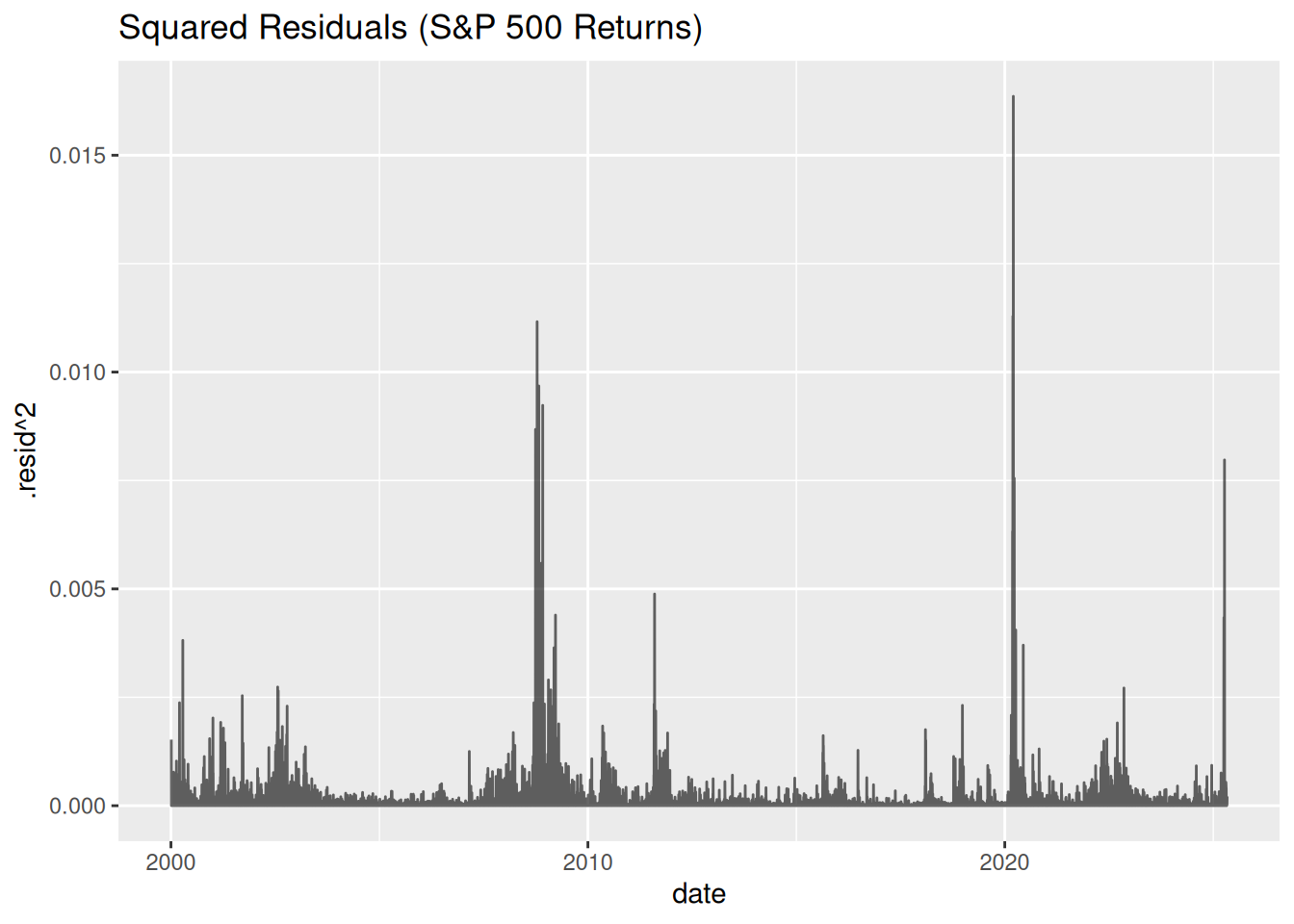

Key Observations:

  • Squared residuals cluster during crises (e.g., 2008 financial crisis, 2020 COVID crash).
  • ARIMA assumes constant variance — clustered residuals violate this, signaling volatility clustering.

Fix: COVID-19 Cases

1. Extract Residuals

First, extract residuals from the ARIMA model:

# For COVID-19 example:
covid_resid <- augment(fit_covid) %>% 
  select(date, .resid)

2. Visual ARCH Test (ACF/PACF of Squared Residuals)

Plot autocorrelation in squared residuals:

covid_resid %>%
  mutate(resid_sq = .resid^2) %>%
  gg_tsdisplay(resid_sq, plot_type = "partial") +
  labs(title = "ACF/PACF of Squared Residuals (COVID-19)")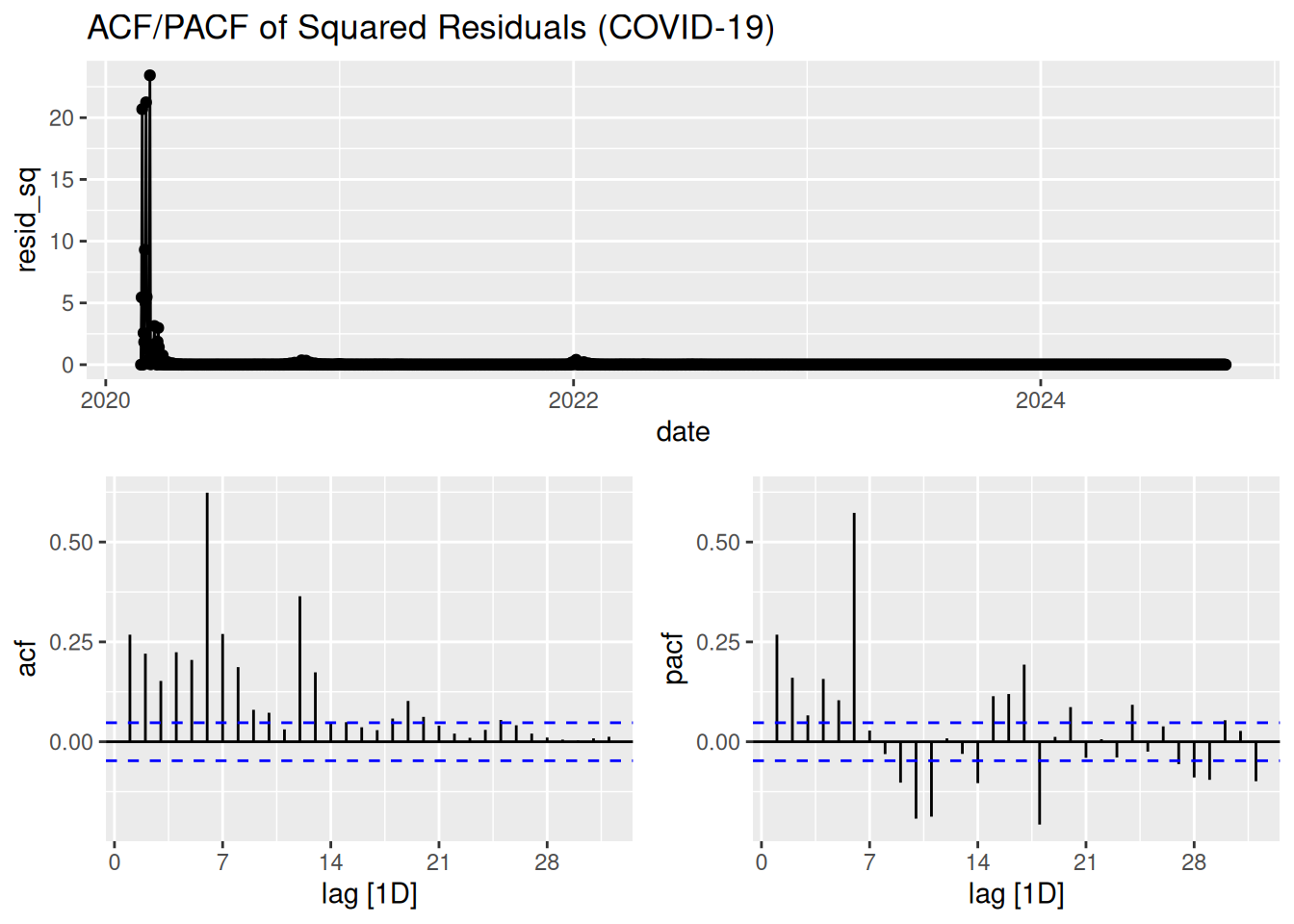

Interpretation:
- Significant spikes at lag 1 or higher → Evidence of ARCH effects.

3. Engle’s ARCH Test

Use the FinTS package to test ARCH effects on residuals:

library(FinTS)  # install.packages("FinTS")

# Extract residual vector
resid_vector <- covid_resid %>% pull(.resid)

# Engle’s ARCH test (lag = 5)
ArchTest(resid_vector, lags = 5, demean = TRUE)

    ARCH LM-test; Null hypothesis: no ARCH effects

data:  resid_vector
Chi-squared = 273.72, df = 5, p-value < 2.2e-16

Conclusion: If \(p < 0.05\), reject the null (ARCH effects exist).

Next Steps: GARCH Modeling

If ARCH effects are detected, use the rugarch package to model volatility:

library(rugarch)  # install.packages("rugarch")

# Fit ARIMA(1,0,1)-GARCH(1,1)
spec <- ugarchspec(
  mean.model = list(armaOrder = c(1,1)), 
  variance.model = list(model = "sGARCH")
)
fit_garch <- ugarchfit(spec, data = resid_vector)
plot(fit_garch, which = 10)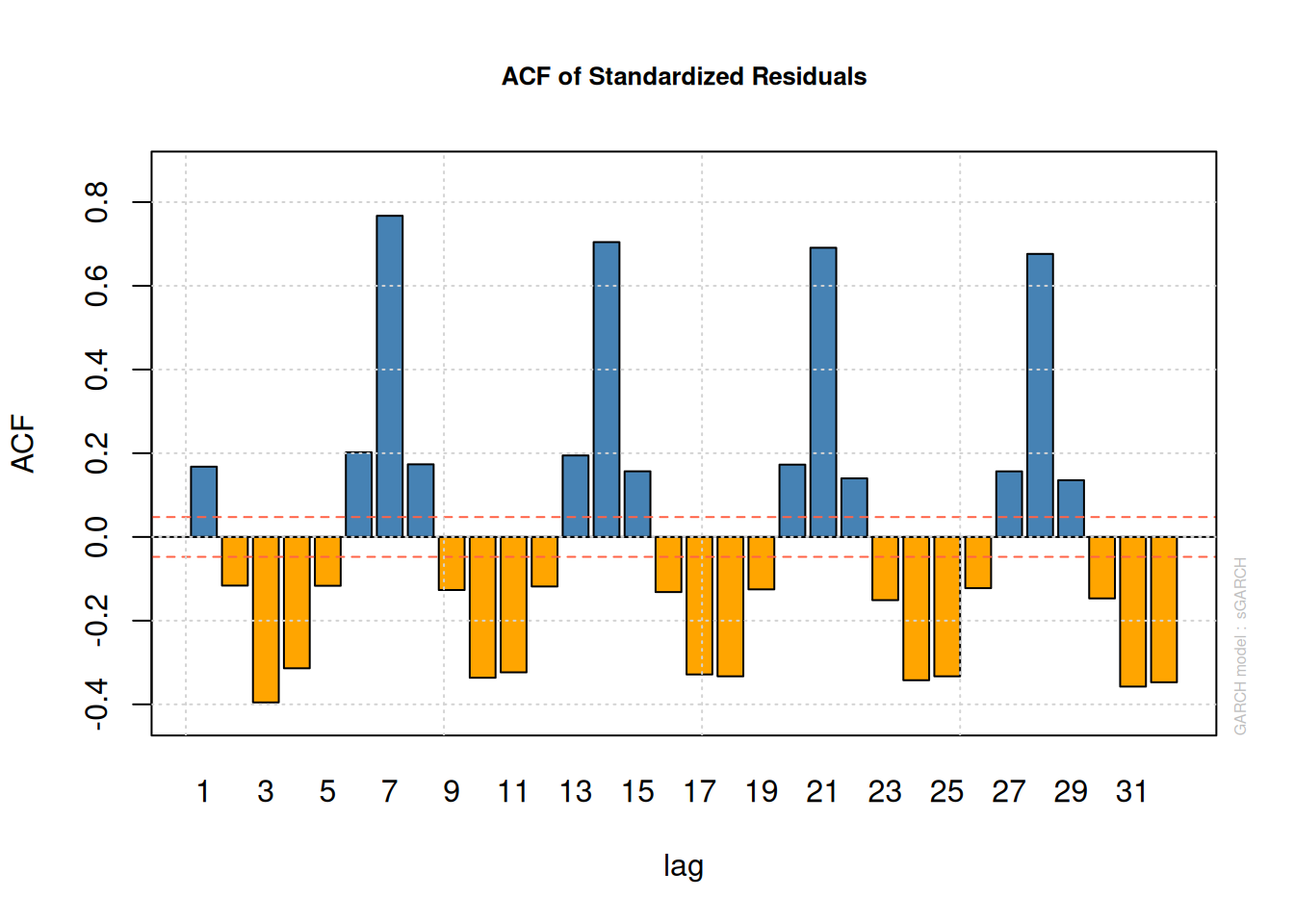

Parameter Stability

Check rolling estimates to assess model stability over time:

roll_fit <- ugarchroll(spec, data = resid_vector, n.ahead = 1, n.start = 1000)
plot(roll_fit, which = 4)  # Rolling parameter estimates

Lab activity: S&P 500 Returns

Repeat the above steps for S&P Returns

# Extract residuals from ARIMA
sp500_resid <- augment(fit_sp500) %>% select(date, .resid)

# Engle’s test
resid_sp500 <- sp500_resid %>% pull(.resid)
ArchTest(resid_sp500, lags = 5, demean = TRUE)

    ARCH LM-test; Null hypothesis: no ARCH effects

data:  resid_sp500
Chi-squared = 1049.2, df = 5, p-value < 2.2e-16
# ACF/PACF of squared residuals
sp500_resid %>%
  mutate(resid_sq = .resid^2) %>%
  gg_tsdisplay(resid_sq, plot_type = "partial")