Activity5

Differencing, Transformations, and Stationarity

What is Stationarity?

A time series is stationary if its statistical properties (mean, variance, autocorrelation) do not change over time. Stationarity is a key assumption for many time series models (e.g., ARIMA). Non-stationary series often exhibit:

• Trends: A long-term increase or decrease in the data.
• Seasonality: Periodic fluctuations.
• Changing Variance: Variability that increases or decreases over time.

Transformations to Achieve Stationarity

1. Differencing: Removes trends by computing the difference between consecutive observations.
   • Formula: \(\nabla X_t = X_t - X_{t-1}\)
2. Log Transformation: Stabilizes multiplicative variance by applying the natural logarithm.
   • Formula: \(Y_t = \log(X_t)\)
3. Box-Cox Transformation: A generalized power transformation that stabilizes variance and can handle non-linear trends.
   • Formula: \(Y_t = \frac{X_t^\lambda - 1}{\lambda}\)

Step 1: Visualize Non-Stationary Data

We start by loading and visualizing a non-stationary time series (Google stock prices).

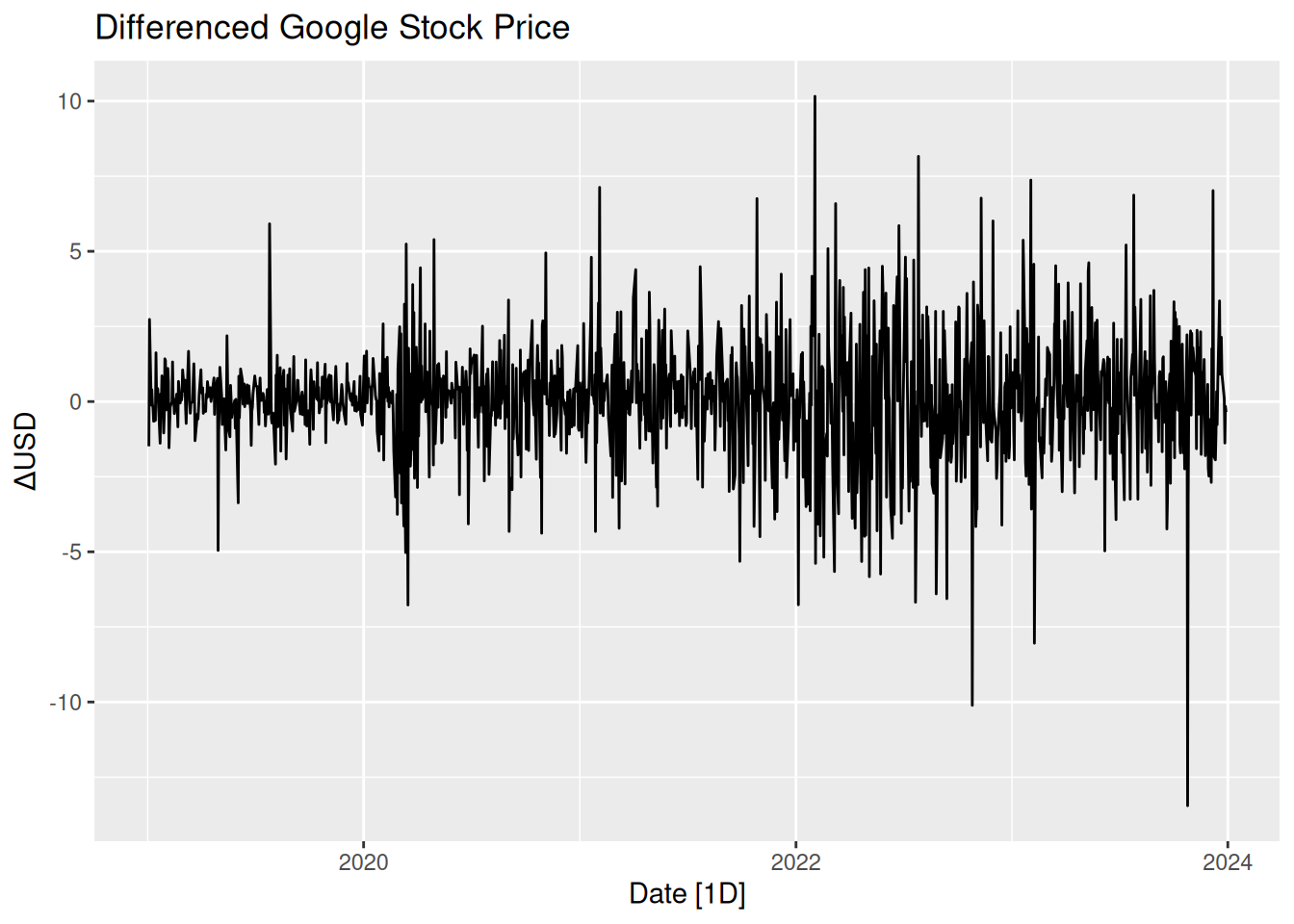
# Load data
google <- read_csv("~/Desktop/Math493Spring25ClassMaterials/data/google.csv")
google_stock <- google |> 
  as_tsibble() |> 
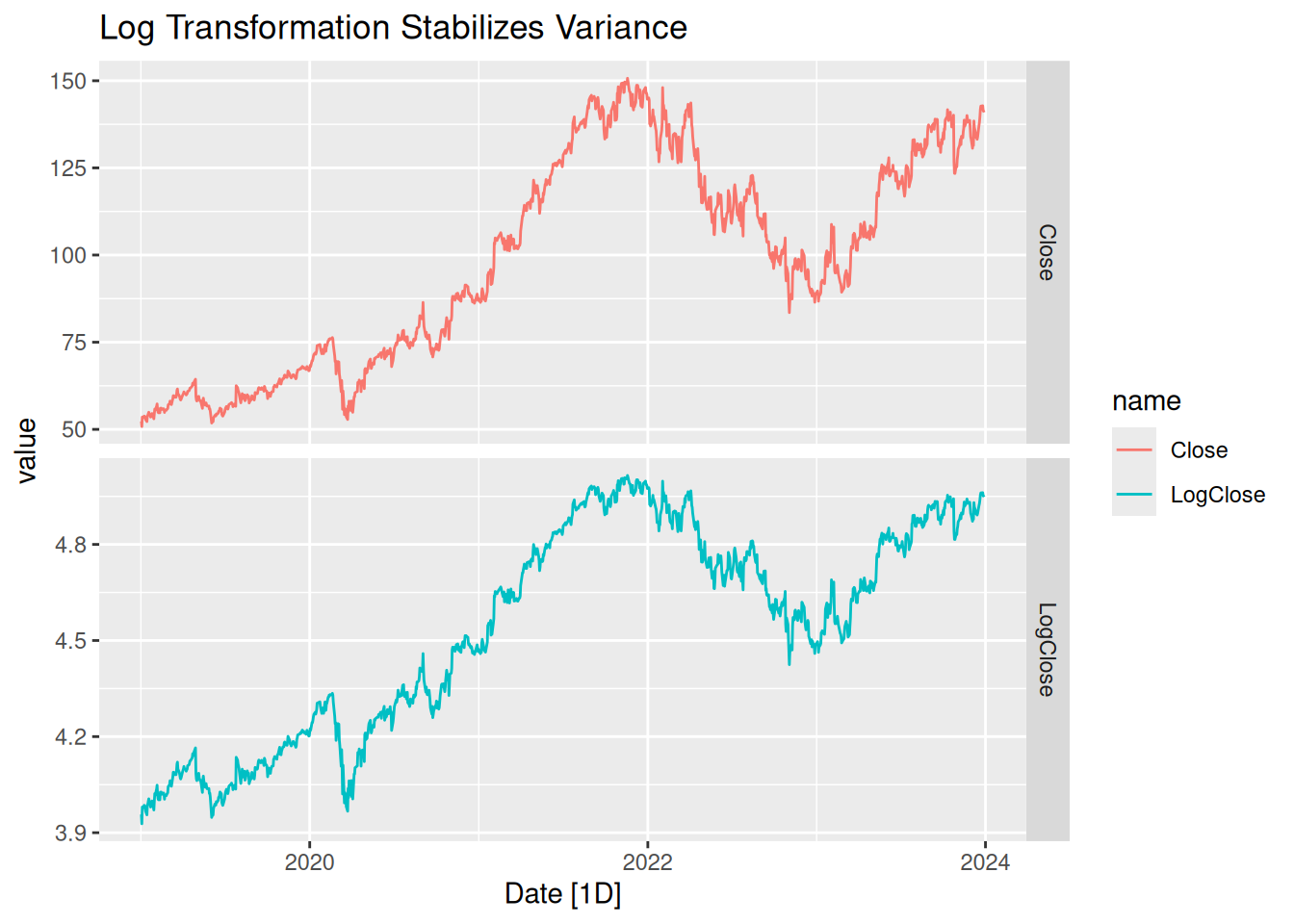
  mutate(LogClose = log(Close))  # Log-transform for later use

# Plot original series
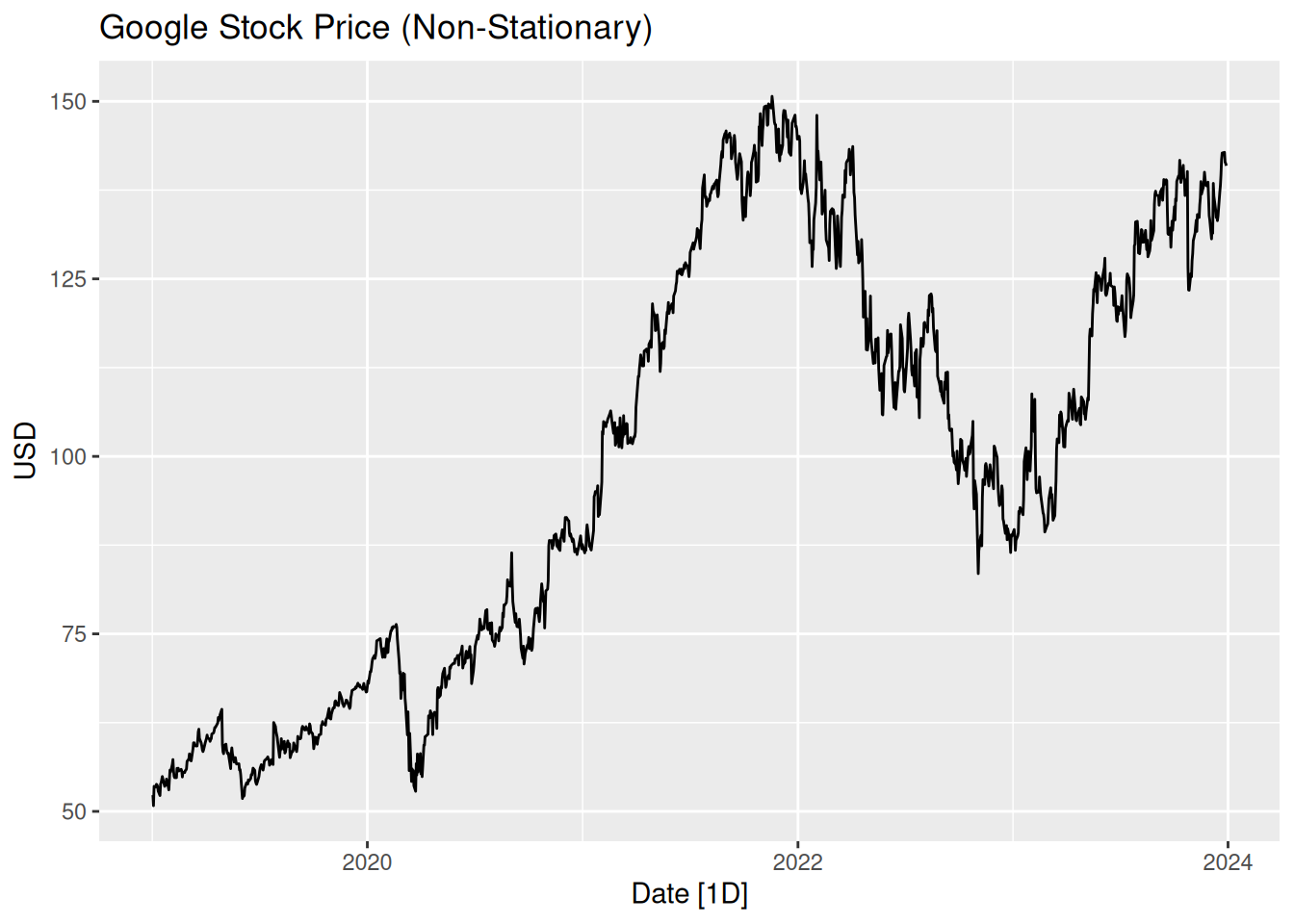
google_stock |>
  autoplot(Close) +
  labs(title = "Google Stock Price (Non-Stationary)", y = "USD")

Observation: The upward trend indicates non-stationarity.

Step 2: Statistical Tests for Stationarity

Use the KPSS test (null hypothesis: stationarity) and ADF test (null hypothesis: unit root) to confirm non-stationarity.

# KPSS test
google_stock |>
  features(Close, unitroot_kpss)

# A tibble: 1 × 2
  kpss_stat kpss_pvalue
      <dbl>       <dbl>
1      10.6        0.01

# Suggested differencing order
google_stock |>
  features(Close, unitroot_ndiffs)

# A tibble: 1 × 1
  ndiffs
   <int>
1      1

Interpretation:

• KPSS p-value < 0.05 ⇒ Reject stationarity.

• unitroot_ndiffs suggests the number of differences required (e.g., 1).

---

Step 3: Apply Differencing

Differencing removes trends by computing the difference between consecutive observations.

# First difference
google_stationary <- google_stock |>
  mutate(DiffClose = difference(Close))

# Plot differenced series
google_stationary |>
  autoplot(DiffClose) +
  labs(title = "Differenced Google Stock Price", y = "ΔUSD")

Observation: The differenced series has a stabilized mean.

Step 4: Apply Log Transformation

Log transformations stabilize multiplicative variance.

# Plot original vs log-transformed series
google_stock |>
  pivot_longer(c(Close, LogClose)) |>
  autoplot(value) +
  facet_grid(name ~ ., scales = "free_y") +
  labs(title = "Log Transformation Stabilizes Variance")

Observation: The log-transformed series shows reduced variance amplification.

---

Step 5: Apply Box-Cox Transformation

The Box-Cox transformation generalizes log and power transformations.

# Estimate optimal lambda
lambda <- google_stock |>
  features(Close, features = guerrero) |>
  pull(lambda_guerrero)

# Apply Box-Cox transformation
google_stock |>
  mutate(BoxCoxClose = box_cox(Close, lambda)) |>
  autoplot(BoxCoxClose) +
  labs(title = "Box-Cox Transformed Series")

Observation: The Box-Cox transformation stabilizes both mean and variance.

---

Lab Activity

Prompt 1: Load and Visualize Data

1. Load the global_economy dataset from the tsibble package.
2. Plot GDP for a specific country (e.g., “United States”). Assess stationarity visually.

Solution:

Prompt 2: Test for Stationarity

1. Use the KPSS test to check for stationarity.
2. Determine the required differencing order using unitroot_ndiffs.

Solution:

Prompt 3: Apply Transformations

1. Apply first differencing to the GDP series.
2. Apply a Box-Cox transformation using Guerrero’s method to estimate λ.
3. Re-test stationarity using the KPSS test.

Solution: